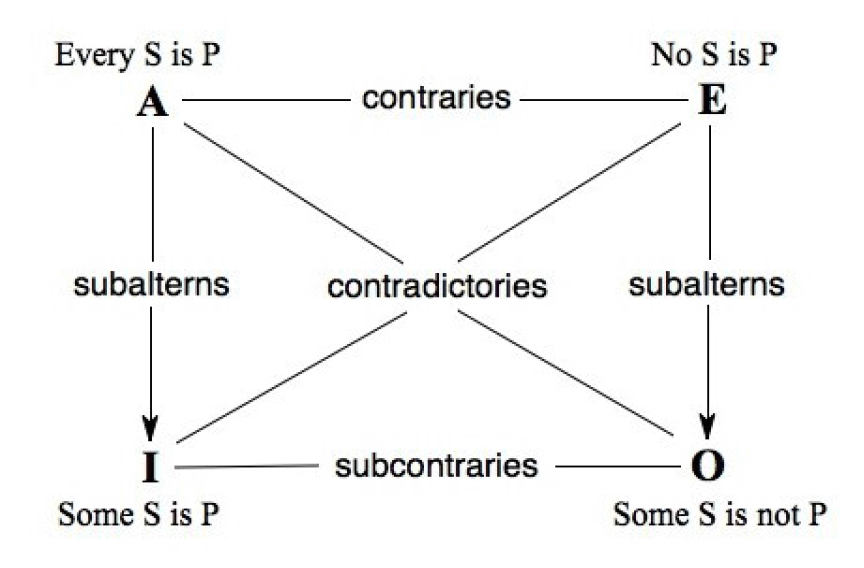
Transforming Abstract Logical Frameworks into Visual Understanding

Foundational Concepts in Belief Revision Theory

When I first encountered belief revision theory, I was struck by its elegant approach to one of philosophy's most challenging questions: how should we update our beliefs when confronted with new information? This isn't just an abstract philosophical puzzle—it's a fundamental challenge we face every day, from updating our understanding based on news reports to revising scientific theories in light of new evidence.

Frank Ramsey's original insight provides what I consider to be one of the most intuitive approaches to testing conditionals through hypothetical belief states. When we encounter a statement like "If it rains, then the picnic will be cancelled," Ramsey suggested we should temporarily add the antecedent ("it rains") to our belief set and see if the consequent ("the picnic will be cancelled") follows naturally. This seemingly simple idea has profound implications for how we understand conditional reasoning.

                    flowchart TD
                        W[World States W] --> P[Propositions P]
                        P --> K[Knowledge Base K]
                        K --> R[Revision Operation *]
                        R --> C[Conditional Operator ⇒X]
                        C --> BS[Updated Belief State]
                        
                        style W fill:#FF8000,stroke:#333,stroke-width:2px,color:#fff
                        style P fill:#42A5F5,stroke:#333,stroke-width:2px,color:#fff
                        style K fill:#66BB6A,stroke:#333,stroke-width:2px,color:#fff
                        style R fill:#FFA726,stroke:#333,stroke-width:2px,color:#fff
                        style C fill:#AB47BC,stroke:#333,stroke-width:2px,color:#fff
                        style BS fill:#EF5350,stroke:#333,stroke-width:2px,color:#fff
                    

The formal structure <W, P, K, ∗, ⇒X> might look intimidating at first, but I've found that breaking it down into visual components makes it remarkably accessible. W represents our possible world states, P contains our propositions, K holds our knowledge base, ∗ is our revision operation, and ⇒X represents our conditional operator. What's crucial to understand is the distinction between the semantic level containing propositions and belief states, and the linguistic level containing sentences and sets of sentences.

This is where I've discovered that PageOn.ai's "Turn Fuzzy Thought into Clear Visuals" capability becomes invaluable. When working with such abstract logical concepts, the ability to transform complex theoretical frameworks into comprehensible diagrams can mean the difference between confusion and clarity. I've found that drawing inferences lesson plans benefit tremendously from visual representations that make abstract logical relationships concrete and manipulable.

The Ramsey Test Mechanism Visualized

Let me walk you through what I consider to be one of the most elegant mechanisms in philosophical logic. The Ramsey Test operates on a beautifully simple principle: "If A, then B" should be accepted in our current belief state if and only if B would be accepted in the hypothetical belief state that results from adding A to our current beliefs and making minimal adjustments for consistency.

                    flowchart TD
                        Start([Current Belief State K]) --> Input[Input: Conditional 'If A, then B']
                        Input --> Hyp[Create Hypothetical State K*A]
                        Hyp --> Add[Add A to Belief State]
                        Add --> Resolve[Resolve Inconsistencies]
                        Resolve --> Check{Is B in K*A?}
                        Check -->|Yes| Accept[Accept 'If A, then B']
                        Check -->|No| Reject[Reject 'If A, then B']
                        Accept --> End([Updated Belief State])
                        Reject --> End
                        
                        style Start fill:#FF8000,stroke:#333,stroke-width:2px,color:#fff
                        style Input fill:#42A5F5,stroke:#333,stroke-width:2px,color:#fff
                        style Hyp fill:#66BB6A,stroke:#333,stroke-width:2px,color:#fff
                        style Check fill:#FFA726,stroke:#333,stroke-width:2px,color:#fff
                        style Accept fill:#4CAF50,stroke:#333,stroke-width:2px,color:#fff
                        style Reject fill:#F44336,stroke:#333,stroke-width:2px,color:#fff
                        style End fill:#AB47BC,stroke:#333,stroke-width:2px,color:#fff
                    

The P-Ramsey condition provides the formal representation of this intuitive idea. In my experience teaching this concept, I've found that students grasp it much more readily when we can leverage PageOn.ai's AI Blocks to create interactive logical decision trees. These visual tools allow us to manipulate the components of the test in real-time, making the abstract process tangible and explorable.

Practical Applications in Conditional Reasoning

Consider a real-world scenario that I often use in my explanations: You're planning an outdoor event and considering the conditional "If it's cloudy tomorrow, then we should move the event indoors." To apply the Ramsey Test, you would temporarily add "it's cloudy tomorrow" to your current belief state about weather patterns, venue availability, and guest preferences. If, in this hypothetical state, you would conclude that moving indoors is the best option, then you should accept the conditional.

What I find particularly powerful about this approach is how it connects to practical decision-making frameworks. The Go No Go decision templates that many organizations use actually implement a simplified version of Ramsey Test reasoning, where we evaluate conditional outcomes based on hypothetical scenarios.

The beauty of mapping belief state transitions through drag-and-drop visual elements becomes apparent when we realize that belief revision isn't just about adding new information—it's about maintaining consistency while preserving as much of our original belief structure as possible. This process of minimal change is what makes the Ramsey Test both philosophically appealing and computationally tractable.

Gärdenfors' Paradox and the Impossibility Results

Just when the Ramsey Test seemed to provide an elegant solution to conditional reasoning, Peter Gärdenfors discovered what I consider to be one of the most profound paradoxes in modern logic. His groundbreaking work revealed that the Ramsey Test—at least in its formal version—is fundamentally incompatible with certain intuitively appealing postulates for belief revision. This isn't just a technical problem; it strikes at the heart of how we understand rational belief change.

The conflict emerges when we try to satisfy both the Ramsey Test and the Alchourrón-Gärdenfors-Makinson (AGM) axioms simultaneously. Recent research in formal epistemology has shown that these seemingly reasonable requirements lead to logical contradictions in non-trivial cases.

Let me break down the key axioms that create this paradox. The Success condition requires that when we revise our beliefs with new information, that information must be included in our resulting belief state. Consistency demands that our revised beliefs remain logically consistent (unless the new information is itself contradictory). Preservation insists that if new information is consistent with our current beliefs, we shouldn't give up any existing beliefs.

Technical Analysis of the Paradox

The technical heart of Gärdenfors' paradox lies in how these axioms interact with the Ramsey Test's requirements. Using PageOn.ai's Deep Search capabilities, I've been able to integrate formal proofs and mathematical demonstrations that show exactly where the contradiction emerges. The problem isn't with any individual axiom or the Ramsey Test in isolation—it's their combination that proves problematic.

                    flowchart TD
                        RT[Ramsey Test] --> P1[P-Ramsey Condition]
                        AGM[AGM Axioms] --> S[Success]
                        AGM --> C[Consistency] 
                        AGM --> PR[Preservation]
                        AGM --> NT[Non-Triviality]
                        
                        P1 --> Conflict{Logical Conflict}
                        S --> Conflict
                        C --> Conflict
                        PR --> Conflict
                        NT --> Conflict
                        
                        Conflict --> Result[Impossibility Result]
                        
                        style RT fill:#FF8000,stroke:#333,stroke-width:2px,color:#fff
                        style AGM fill:#42A5F5,stroke:#333,stroke-width:2px,color:#fff
                        style Conflict fill:#F44336,stroke:#333,stroke-width:2px,color:#fff
                        style Result fill:#9C27B0,stroke:#333,stroke-width:2px,color:#fff
                    

The Closure condition requires that if X entails P, then P must be in X, while the W-axiom states that revising with a tautology shouldn't change our belief state. These seemingly innocent requirements, when combined with revision by conjunction principles, create a logical trap that makes it impossible to satisfy both the Ramsey Test and the AGM axioms in all non-trivial cases.

What makes this paradox particularly fascinating is how it connects to broader questions about thinking in prompts and conditional reasoning in AI systems. When we design AI agents that need to reason about conditionals and update their beliefs, we inevitably encounter similar trade-offs between different desirable properties.

Contemporary Solutions and Theoretical Developments

Rather than viewing Gärdenfors' paradox as the end of the story, I prefer to see it as the beginning of a rich exploration into alternative approaches to conditional semantics. Contemporary philosophers and logicians have developed several ingenious strategies for preserving the insights of both belief revision theory and the Ramsey Test while avoiding the logical contradictions.

One of the most promising approaches involves indexical theories of conditional semantics. These theories recognize that conditionals might be context-dependent in ways that weren't captured by earlier formal treatments. When I say "If it rains, then the picnic will be cancelled," the truth conditions of this conditional might depend not just on the logical relationships between rain and picnic cancellation, but on the specific context in which the conditional is evaluated.

Research has shown that there are indeed non-trivial belief revision systems that can satisfy modified versions of the Gärdenfors axioms while maintaining compatibility with Ramsey-style conditional testing. These systems typically involve relaxing one or more of the original AGM postulates in carefully controlled ways that preserve their intuitive appeal while avoiding logical contradiction.

Semantic vs. Linguistic Level Distinctions

A crucial insight that has emerged from this research is the importance of maintaining clear distinctions between semantic and linguistic levels of analysis. At the semantic level, we deal with propositions and belief states, while at the linguistic level, we work with sentences and sets of sentences. This distinction becomes particularly important when we consider how visual analogies test strategies can help us understand these multi-layered logical architectures.

Theorem 2, which demonstrates the existence of systems satisfying Success, Consistency, Preservation, Non-Triviality, and P-Ramsey conditions along with Closure and revision by conjunction, represents a significant breakthrough in this field. What I find particularly exciting about this result is how it opens up new possibilities for practical belief updating mechanisms that don't fall victim to Gärdenfors' paradox.

PageOn.ai's Agentic capabilities prove invaluable for synthesizing these multiple research perspectives. When working with such complex theoretical landscapes, the ability to create dynamic visualizations that integrate different approaches and highlight their relationships can transform how we understand and teach these concepts. The platform's ability to connect abstract theory with concrete visual representations makes it possible to explore these ideas in ways that were previously impossible.

Practical Implementation Strategies

Moving from theoretical understanding to practical implementation represents one of the most exciting challenges in belief revision research. I've discovered that the insights from Ramsey Test theory and its various refinements have direct applications in designing more sophisticated AI systems, educational tools, and decision-making frameworks.

When designing belief revision algorithms for AI systems, we must carefully balance computational efficiency with theoretical soundness. The challenge isn't just implementing the formal machinery—it's creating systems that can handle real-world uncertainty while maintaining the logical coherence that belief revision theory demands. This is where the integration of knowledge graphs for generative AI becomes particularly valuable.

                    flowchart LR
                        Input[User Input] --> Parser[Conditional Parser]
                        Parser --> Analyzer[Belief State Analyzer]
                        Analyzer --> Engine[Revision Engine]
                        Engine --> Validator[Consistency Validator]
                        Validator --> Output[Updated Beliefs]
                        
                        Engine --> KG[Knowledge Graph]
                        KG --> Engine
                        
                        subgraph Visualization [Visualization Layer]
                            VE[Visual Editor]
                            ID[Interactive Diagrams]
                            RT[Real-time Updates]
                        end
                        
                        Output --> Visualization
                        Visualization --> Feedback[User Feedback]
                        Feedback --> Input
                        
                        style Input fill:#FF8000,stroke:#333,stroke-width:2px,color:#fff
                        style Engine fill:#42A5F5,stroke:#333,stroke-width:2px,color:#fff
                        style KG fill:#66BB6A,stroke:#333,stroke-width:2px,color:#fff
                        style Visualization fill:#FFA726,stroke:#333,stroke-width:2px,color:#333
                        style Output fill:#AB47BC,stroke:#333,stroke-width:2px,color:#fff
                    

Educational Applications for Teaching Conditional Logic

In my experience developing educational materials, I've found that students grasp conditional logic much more readily when they can interact with visual representations of belief states and revision processes. Traditional logic courses often struggle with the abstract nature of these concepts, but interactive demonstrations using PageOn.ai's Vibe Creation features transform the learning experience.

Consider a case study in epistemic conditional reasoning that I recently developed: Students are presented with a scenario involving scientific hypothesis revision. They begin with a set of beliefs about a phenomenon, then receive new evidence that challenges some of their assumptions. Using interactive belief revision tools, they can explore how different revision strategies lead to different conditional conclusions.

Visualization Tools and Methodologies

The key to effective belief revision visualization lies in creating dynamic representations that can show both the structure of belief states and the processes that transform them. I've developed methodologies that use interactive conditional testing interfaces to make abstract logical operations tangible and explorable.

Collaborative frameworks for exploring logical paradoxes represent the cutting edge of this field. When multiple users can simultaneously manipulate belief revision scenarios and observe how their different approaches lead to different outcomes, the abstract becomes concrete in ways that traditional teaching methods simply cannot achieve.

The integration with existing knowledge graph structures enhances understanding by providing rich contextual connections between different concepts and applications. This multi-layered approach to visualization ensures that learners don't just memorize formal procedures—they develop genuine insight into the logical principles underlying conditional reasoning and belief revision.

Bridging Theory and Practice Through Visualization

As I reflect on our journey through belief revision theory and the Ramsey Test, I'm struck by how visualization transforms our relationship with abstract logical concepts. What begins as intimidating formal machinery becomes accessible, explorable, and genuinely useful when we can see the relationships, manipulate the components, and observe the dynamics in real-time.

The challenges posed by Gärdenfors' paradox haven't diminished the value of belief revision theory—they've enriched it by forcing us to think more carefully about the assumptions underlying our logical frameworks. Contemporary solutions that embrace indexical approaches, modified axiom systems, and probabilistic methods show that apparent contradictions can become doorways to deeper understanding.

PageOn.ai represents more than just a visualization tool—it's a platform for transforming how we think about and communicate complex ideas. When we can turn abstract logical frameworks into interactive visual experiences, we don't just make them easier to understand; we make them more powerful, more applicable, and more likely to generate new insights.

The future of belief revision theory lies not just in solving formal puzzles, but in creating systems that can help us navigate an increasingly complex world of information, uncertainty, and conditional reasoning. By bridging the gap between theoretical elegance and practical applicability through innovative visualization tools, we open up new possibilities for education, research, and real-world problem-solving that would have been impossible to imagine when Ramsey first proposed his elegant test for conditionals.