Demystifying Material Conditional Paradoxes: When Logic Defies Intuition
Exploring the Fascinating World Where Classical Logic Challenges Common Sense
I've always been fascinated by how formal logic can produce results that feel completely counterintuitive. Today, I want to take you on a journey through one of the most perplexing aspects of classical logic: the paradoxes of material implication. These aren't just academic curiosities—they reveal fundamental tensions between how we naturally reason and how formal logical systems operate.
The Foundation of Material Conditionals in Classical Logic
When I first encountered material conditionals in my logic studies, I was struck by their elegant simplicity—and their profound strangeness. A material conditional is essentially an "if-then" statement in formal logic, represented as P → Q (read as "if P then Q"). What makes these statements so fascinating is how they're evaluated for truth.
The Truth Table Structure
The foundation of understanding material conditional paradoxes lies in their truth table. Let me show you the four possible combinations:

What's remarkable about this truth table is that a conditional is false only when we have a true antecedent (P) and a false consequent (Q). In every other case—including when the antecedent is false—the conditional is considered true. This is where our journey into paradox begins, and where tools like PageOn.ai's AI Blocks become invaluable for visualizing these abstract relationships in ways that make intuitive sense.
The historical development from Aristotelian logic to modern propositional calculus reveals how these truth conditions emerged not from arbitrary choice, but from the need to create consistent logical systems. Yet as we'll see, this consistency comes at the cost of sometimes defying our natural reasoning patterns. Understanding drawing inferences lesson plans can help illuminate how we naturally process conditional statements versus how formal logic demands we evaluate them.
The Two Core Paradoxes Revealed
In my years of studying logic, I've found that the paradoxes of material implication are best understood through concrete examples. These aren't just theoretical curiosities—they reveal fundamental issues about how formal systems can diverge from intuitive reasoning.
The Structure of Both Paradoxes
flowchart TD
A[Material Conditional P → Q] --> B{Evaluate Truth}
B --> C[P is False]
B --> D[Q is True]
C --> E[Conditional is TRUE
Regardless of Q]
D --> F[Conditional is TRUE
Regardless of P]
E --> G[Paradox 1: False Antecedent]
F --> H[Paradox 2: True Consequent]
style A fill:#FF8000,stroke:#333,stroke-width:2px,color:#fff
style G fill:#EF4444,stroke:#333,stroke-width:2px,color:#fff
style H fill:#EF4444,stroke:#333,stroke-width:2px,color:#fff
The False Antecedent Paradox
Consider this statement: "If the moon is made of cheese, then I am Napoleon." According to classical logic, this statement is true because the antecedent (the moon is made of cheese) is false.
This feels wrong to our intuition. How can a statement about cheese moons and Napoleon be logically valid simply because one part is false?
The True Consequent Paradox
Similarly, "If grass is purple, then snow is white" is deemed logically valid because the consequent (snow is white) is true, regardless of the absurd antecedent.
Again, our intuition rebels. Why should facts about snow's color validate statements about purple grass?

What I find most intriguing about these paradoxes is how they expose the gap between logical validity and meaningful content. When I use PageOn.ai's Vibe Creation tools to visualize these concepts, the disconnect becomes even more apparent—we can create compelling visual demonstrations that show how formal logic can accept statements that feel meaningless to human reasoning.
These paradoxes aren't bugs in the logical system—they're features that emerge from the need for consistency and completeness in formal logic. However, they do raise profound questions about whether classical logic adequately captures human reasoning, especially when we consider how optical illusions similarly reveal gaps between perception and reality.
The Principle of Explosion and Its Consequences
One of the most dramatic consequences of material conditional paradoxes is their relationship to what logicians call the "principle of explosion" (ex falso quodlibet). This principle states that from a contradiction, anything follows. I've always found this to be one of the most unsettling aspects of classical logic.
How Explosion Works
flowchart TD
A[Contradiction: P ∧ ¬P] --> B[Assume any statement Q]
B --> C[From P ∧ ¬P, we can derive P]
C --> D[From P, we get P ∨ Q
by disjunction introduction]
D --> E[From P ∧ ¬P, we also get ¬P]
E --> F[From ¬P and P ∨ Q,
we derive Q by disjunctive syllogism]
F --> G[Therefore: Any statement Q follows
from a contradiction]
style A fill:#EF4444,stroke:#333,stroke-width:2px,color:#fff
style G fill:#10B981,stroke:#333,stroke-width:2px,color:#fff
style F fill:#FF8000,stroke:#333,stroke-width:2px,color:#fff
C.I. Lewis's Insight
C.I. Lewis, who first systematically identified these logical peculiarities, showed how material conditionals enable explosive reasoning. If we accept that false antecedents make conditionals true, then any contradiction can "prove" absolutely anything.
For instance, if we somehow derived both "Socrates is mortal" and "Socrates is not mortal," we could then prove that "The number 7 is purple" or "All unicorns speak French."

What makes this particularly troubling is how it connects to the material conditional paradoxes. Since "If P then Q" is true whenever P is false, and since contradictions make everything false (and therefore true), we end up in a situation where inconsistent premises validate any conclusion whatsoever. This is where PageOn.ai's content expression capabilities become invaluable—crafting compelling visual narratives around these explosion examples helps make the abstract concrete.
The practical implications are staggering. In any formal system that admits even a single contradiction, the entire system becomes trivial—every statement becomes provable. This is why maintaining consistency is so crucial in mathematics, computer science, and logic model PowerPoint templates used in formal reasoning contexts.
When Intuition Clashes with Formal Logic
Throughout my exploration of these paradoxes, I've been continually struck by the profound mismatch between how we naturally understand "if-then" statements and how classical logic defines them. This isn't just an academic issue—it has real implications for how we communicate, reason, and build logical systems.
Natural vs. Formal Interpretation
The Negation Problem
Consider the statement: "If God exists, all criminals will go to heaven." In classical logic, the negation of this conditional is "God exists and not all criminals will go to heaven." But intuitively, many people would simply deny the conditional by saying "That's not true" without accepting the existence of God.
This reveals how classical logic forces us into ontological commitments that natural language reasoning typically avoids.
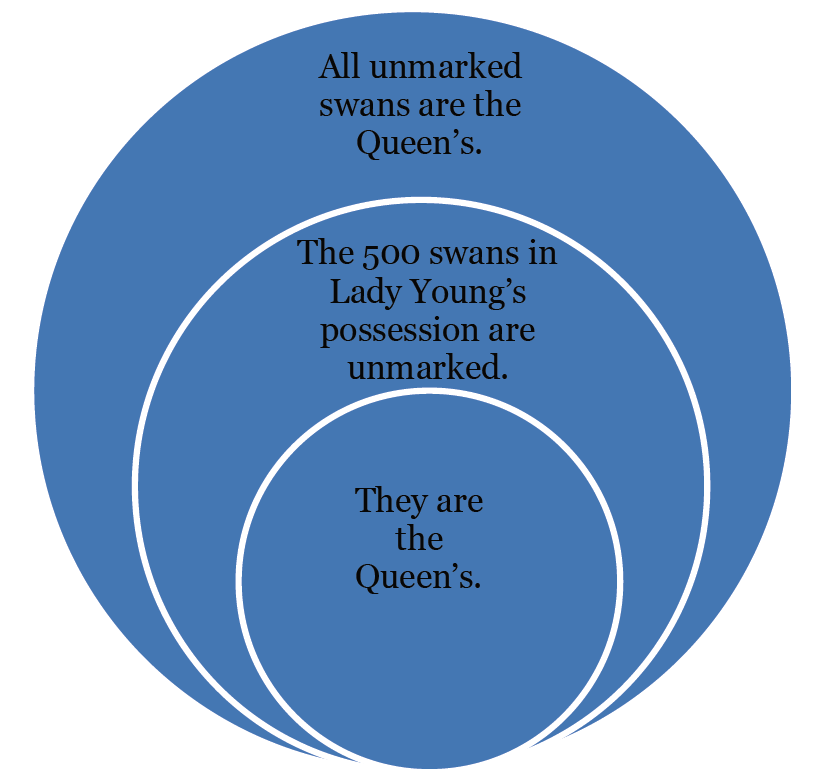
What I find particularly fascinating is how this mismatch affects everyday reasoning. When someone says "If it rains, I'll stay home," they're implying a causal or intentional connection between rain and their decision. The material conditional, however, treats this as true even if they stay home for completely unrelated reasons, or if it doesn't rain at all.
This is where PageOn.ai's asset integration features become incredibly valuable. By integrating real-world reasoning examples and visualizing the differences between natural and formal interpretation, we can better understand why these paradoxes feel so counterintuitive. The challenge isn't that formal logic is wrong—it's that it serves different purposes than everyday reasoning.
Understanding these differences is crucial for anyone working with formal systems, whether in mathematics, computer science, or philosophy. It's also why caliper test visual analogy answers often require careful distinction between logical and intuitive reasoning patterns.
Philosophical and Practical Implications
The paradoxes of material implication raise fundamental questions about the nature of logic, reasoning, and meaning. In my exploration of these issues, I've come to appreciate how they challenge some of our most basic assumptions about what constitutes valid reasoning.
Soundness vs. Validity
Classical logic distinguishes between valid arguments (where conclusions follow from premises) and sound arguments (where premises are also true). The paradoxes show how this distinction can produce valid but meaningless arguments.
- • Valid but unsound: "If unicorns exist, then 2+2=4"
- • The truth of mathematics doesn't depend on mythical creatures
- • Yet classical logic accepts this as valid reasoning
AI and Automated Reasoning
These paradoxes have profound implications for artificial intelligence systems that rely on classical logic for reasoning and decision-making.
- • Expert systems must handle contradictory information
- • Database queries can return unexpected results
- • Machine learning systems need robust logical foundations
Domains Affected by Material Conditional Paradoxes
graph TD
A[Material Conditional Paradoxes] --> B[Philosophy of Logic]
A --> C[Computer Science]
A --> D[Mathematics]
A --> E[Artificial Intelligence]
A --> F[Linguistics]
B --> B1[Meaning and Truth]
B --> B2[Alternative Logics]
C --> C1[Formal Verification]
C --> C2[Database Systems]
D --> D1[Proof Theory]
D --> D2[Set Theory]
E --> E1[Expert Systems]
E --> E2[Natural Language Processing]
F --> F1[Semantics]
F --> F2[Pragmatics]
style A fill:#FF8000,stroke:#333,stroke-width:3px,color:#fff
style B fill:#8B5CF6,stroke:#333,stroke-width:2px,color:#fff
style C fill:#10B981,stroke:#333,stroke-width:2px,color:#fff
style D fill:#F59E0B,stroke:#333,stroke-width:2px,color:#fff
style E fill:#EF4444,stroke:#333,stroke-width:2px,color:#fff
style F fill:#3B82F6,stroke:#333,stroke-width:2px,color:#fff

What strikes me most about these implications is how they force us to confront the limits of formal systems. Classical logic excels at preserving truth and maintaining consistency, but it struggles with relevance and meaning. This has led to the development of alternative logical systems, each attempting to address different aspects of the paradoxes.
Using PageOn.ai's AI Blocks to structure these complex philosophical arguments helps clarify the relationships between different positions and their implications. The visual approach is particularly valuable when exploring how evolution of law visualization might benefit from understanding these logical foundations, especially in legal reasoning systems.
Modern Solutions and Ongoing Debates
The recognition of these paradoxes hasn't led to the abandonment of classical logic, but rather to the development of alternative systems that attempt to address its counterintuitive aspects. I've found that each proposed solution offers insights while introducing its own trade-offs.
| Logical System | Key Innovation | Advantages | Limitations |
|---|---|---|---|
| Strict Conditional Logic | Requires necessity, not just truth preservation | Eliminates both paradoxes | Complex modal semantics |
| Relevance Logic | Demands meaningful connection between premises and conclusion | Intuitive relevance requirements | Loses some classical theorems |
| Possible Worlds Semantics | Truth evaluated across possible scenarios | Rich semantic framework | Ontological commitments |
| Paraconsistent Logic | Tolerates contradictions without explosion | Handles inconsistent information | Weakens classical reasoning power |
C.I. Lewis's Strict Conditional
Lewis proposed that "If P then Q" should mean "Necessarily, if P then Q" rather than merely "Either not-P or Q." This strict conditional requires that Q follows necessarily from P, not just that they happen to have compatible truth values.
While this eliminates the paradoxes, it introduces the complexities of modal logic and raises questions about what constitutes "necessity" in different contexts.
What I find most interesting about these alternative approaches is that none has completely replaced classical logic. Instead, different systems prove useful for different purposes. Classical logic remains dominant in mathematics and computer science, while relevance logic appeals to those concerned with meaningful reasoning, and paraconsistent logic proves valuable in contexts where contradictory information must be handled gracefully.
PageOn.ai's visualization capabilities are particularly valuable here for illustrating the trade-offs between different logical frameworks. The ability to create clear visual comparisons helps illuminate why the debate continues and why no single solution has emerged as universally superior. Each system makes different assumptions about what logic should accomplish and what trade-offs are acceptable.
Applications in Contemporary Logic and AI
The practical implications of material conditional paradoxes extend far beyond academic philosophy. In my work with various logical systems, I've encountered these issues in contexts ranging from software engineering to educational technology, demonstrating their ongoing relevance in our digital age.
Programming and Formal Verification
In software development, conditional statements must handle edge cases gracefully. The paradoxes highlight why simple if-then logic can produce unexpected behaviors:
- • Database queries with null values
- • Exception handling in conditional blocks
- • Formal specification languages
- • Automated testing frameworks
Educational Technology
Teaching logic requires addressing these counterintuitive aspects to prevent student confusion and build robust understanding:
- • Interactive logic tutoring systems
- • Automated reasoning in educational software
- • Assessment of logical reasoning skills
- • Visualization of abstract concepts
From Theory to Practice: Application Pipeline
flowchart LR
A[Theoretical Understanding] --> B[Identify Paradox Contexts]
B --> C[Design Robust Systems]
C --> D[Implement Solutions]
D --> E[Test Edge Cases]
E --> F[Educational Integration]
B --> B1[Database Queries]
B --> B2[AI Reasoning]
B --> B3[Formal Verification]
C --> C1[Alternative Logics]
C --> C2[Exception Handling]
C --> C3[Relevance Checking]
style A fill:#FF8000,stroke:#333,stroke-width:2px,color:#fff
style F fill:#10B981,stroke:#333,stroke-width:2px,color:#fff
Machine Learning and Natural Language Processing
Modern AI systems must navigate the gap between formal logic and natural language understanding. The paradoxes highlight why purely logical approaches to language understanding can fail:
- • Contextual interpretation
- • Causal reasoning
- • Pragmatic inference
- • Probabilistic logic
- • Context-aware systems
- • Hybrid approaches
- • Chatbots and assistants
- • Automated reasoning
- • Knowledge graphs

One area where I've seen these issues become particularly relevant is in automated theorem proving and formal verification systems. These systems must balance the rigor of classical logic with the need to produce meaningful results. The paradoxes remind us that logical validity doesn't always align with practical usefulness.
This is where PageOn.ai's thought-to-visual conversion tools become invaluable for transforming these abstract logical concepts into accessible visual learning materials. Whether we're designing educational software, building AI reasoning systems, or simply trying to communicate complex logical ideas, the ability to visualize the relationships between formal logic and intuitive reasoning helps bridge the gap between theory and practice.
Transform Your Visual Expressions with PageOn.ai
Whether you're grappling with logical paradoxes, designing educational materials, or building AI reasoning systems, PageOn.ai empowers you to transform complex abstract concepts into clear, compelling visual expressions. From truth tables to philosophical arguments, make the invisible visible.
Start Creating with PageOn.ai TodayEmbracing the Paradox
Throughout this exploration of material conditional paradoxes, I've come to appreciate how they illuminate fundamental tensions in human reasoning. These aren't merely technical curiosities—they reveal deep questions about the nature of logic, meaning, and truth that continue to shape how we build formal systems and understand reasoning itself.
The paradoxes remind us that formal logic serves specific purposes: ensuring consistency, preserving truth, and enabling mechanical reasoning. While this sometimes produces counterintuitive results, it also provides the foundation for mathematics, computer science, and rigorous argumentation. The challenge isn't to eliminate these paradoxes but to understand their role and limitations.
As we continue to develop AI systems, educational technologies, and formal reasoning tools, these insights remain crucial. PageOn.ai's powerful visualization capabilities offer new ways to make these abstract concepts accessible, helping bridge the gap between formal logic and intuitive understanding. By transforming complex logical relationships into clear visual expressions, we can better navigate the fascinating world where classical logic meets human reasoning.
You Might Also Like
Building Trust in AI-Generated Marketing Content: Transparency, Security & Credibility Strategies
Discover proven strategies for establishing authentic trust in AI-generated marketing content through transparency, behavioral intelligence, and secure data practices.
Google's 9-Hour Prompt Engineering Path to AI Mastery | Complete Visual Guide
Master AI communication through Google's comprehensive 9-hour prompt engineering framework. Learn visual strategies for effective AI interaction and professional success.
Prompt Chaining Techniques That Scale Your Business Intelligence | Advanced AI Strategies
Master prompt chaining techniques to transform complex business intelligence workflows into scalable, automated insights. Learn strategic AI methodologies for data analysis.
Transform Your AI Results by Mastering the Art of Thinking in Prompts | Strategic AI Communication
Master the strategic mindset that transforms AI interactions from fuzzy requests to crystal-clear outputs. Learn professional prompt engineering techniques that save 20+ hours weekly.
