Mapping Conditional Logic's Possible Worlds
From Abstract Philosophy to Visual Understanding
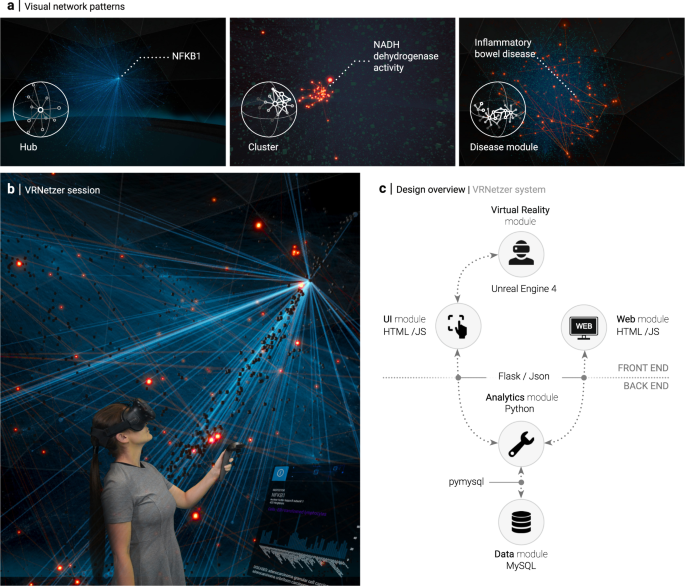
I invite you to explore the fascinating realm of variably strict conditional logic, where abstract philosophical concepts meet practical visualization. Together, we'll discover how to transform complex logical relationships into clear, intuitive visual expressions that make possible worlds semantics accessible and actionable.
Demystifying Variably Strict Conditional Logic
When I first encountered variably strict conditional logic, I realized we were dealing with something far more nuanced than traditional logical frameworks could handle. The core challenge lies in understanding why context-dependent conditionals resist simple true-or-false evaluations. Traditional logic struggles with statements like "If Maddy drinks beer, she won't have a soda" because the truth depends entirely on which possible worlds we consider relevant to our evaluation.

David Lewis and Robert Stalnaker revolutionized our understanding by introducing the concept of "closest possible worlds." As Stanford Encyclopedia of Philosophy explains, their approach recognizes that evaluating a conditional requires us to extend our accessibility relation to the most similar worlds where the antecedent holds true. This isn't just academic theory—it's a fundamental insight into how we naturally reason about hypothetical situations.
The Accessibility Relation Problem
I find it helpful to think of accessibility relations as bridges between worlds. The challenge is that these bridges aren't fixed—they shift based on what we're considering. When we evaluate "If A, then B," we don't just look at any world where A is true; we look at the A-worlds that are most similar to our current situation.
World Accessibility Relations
graph TD
W[Current World w] --> A1[A-world 1
Closest]
W --> A2[A-world 2
Moderately Close]
W --> A3[A-world 3
Distant]
A1 --> B1[B holds true]
A2 --> B2[B holds true]
A3 --> B3[B fails]
classDef current fill:#FF8000,stroke:#333,stroke-width:3px,color:#fff
classDef closest fill:#42A5F5,stroke:#333,stroke-width:2px,color:#fff
classDef moderate fill:#66BB6A,stroke:#333,stroke-width:2px,color:#fff
classDef distant fill:#FFA726,stroke:#333,stroke-width:2px,color:#fff
classDef outcome fill:#E1F5FE,stroke:#333,stroke-width:1px
class W current
class A1 closest
class A2 moderate
class A3 distant
class B1,B2,B3 outcome
Consider a practical example that illustrates this beautifully: imagine we're evaluating "If it rains tomorrow, the picnic will be cancelled." The truth of this conditional doesn't depend on bizarre rain-worlds where people have picnics in hurricanes. Instead, we focus on the most normal, expected rain scenarios. This is where knowledge graphs for generative AI become invaluable—they help us map these similarity relationships systematically.
What I find most compelling about this approach is how it mirrors our natural reasoning processes. When you think about "what would happen if," you instinctively focus on the most plausible scenarios, not the most outlandish ones. PageOn.ai's AI Blocks feature allows us to create intuitive similarity maps that capture this natural reasoning process, transforming abstract logical relationships into visual frameworks that anyone can understand and work with.
The Architecture of Possible Worlds Semantics
Building the formal framework for possible worlds semantics feels like constructing a sophisticated navigation system for abstract space. At its core, we're working with sf-models—structures that combine worlds, selection functions, and valuation functions into a coherent system for evaluating conditional statements.

The Formal Structure
An sf-model consists of three essential components: a set of possible worlds (W), a selection function (f), and a valuation function (V). The selection function is particularly crucial—it determines which worlds are accessible from any given world when evaluating a conditional. This isn't arbitrary; it's based on similarity relations that context helps define.
SF-Model Components
What fascinates me most is how context determines which worlds are "reachable" for evaluation. This isn't a static relationship—it's dynamic and responsive. When we accept one conditional, it literally changes the landscape for evaluating subsequent conditionals. This is what researchers call the "dynamic updating" of conditional contexts.
Dynamic Conditional Updating
Here's how accepting one conditional reshapes our evaluation space for others:
sequenceDiagram
participant C as Context c
participant W as World w
participant A as Antecedent A
participant B as Consequent B
participant U as Updated Context c[A→B]
C->>W: Initial evaluation space
W->>A: Consider A-worlds
A->>B: Evaluate A→B
B->>U: Accept conditional
U->>W: Revised evaluation space
Note over U,W: New accessibility relations
W->>U: Future conditionals evaluated in updated context
The relationship between indicative and counterfactual conditionals becomes clearer when we map these world-ordering relations visually. Indicative conditionals ("If it's raining, the streets are wet") typically focus on worlds we expect to be actual, while counterfactuals ("If it had rained, the streets would be wet") explore worlds we know to be non-actual but similar in relevant respects.
This is where PageOn.ai's Deep Search capabilities become invaluable. By integrating formal logic diagrams with accessible explanations, we can create visual representations that maintain mathematical rigor while remaining intuitive. I've found that this approach helps bridge the gap between abstract theory and practical understanding, making complex logical structures accessible to broader audiences.
Key Insight: Context as Navigator
Think of context as a sophisticated GPS system for logical space. Just as your GPS considers current traffic conditions, road closures, and your destination to calculate the best route, context considers current beliefs, relevant similarities, and evaluative goals to determine which possible worlds matter for assessing a conditional statement.
From Formal Logic to Practical Applications
The beauty of variably strict conditional logic lies not just in its theoretical elegance, but in its profound practical applications. I've discovered that decision-making frameworks naturally mirror conditional logic structures, especially when we're dealing with uncertain outcomes and context-dependent choices.

Decision-Making Frameworks
When we use Go No Go decision templates, we're essentially applying conditional logic principles. Each decision point represents a conditional: "If condition X holds, then we proceed to option Y." The variably strict approach helps us understand that the strength of these conditionals depends on context—market conditions, resource availability, strategic priorities.
Conditional Decision Strength by Context
In AI safety applications, conditional reasoning becomes crucial for building robust guardrails and exception handling. When I work with visual framework for AI safety, I'm essentially mapping conditional structures: "If the AI encounters scenario A, then safety protocol B should activate." The variably strict approach helps us understand that these safety conditionals must be sensitive to context while maintaining their protective function.
AI Safety Conditional Framework
flowchart TD
AI[AI System] --> D1{Context Detection}
D1 --> C1[Low Risk Context]
D1 --> C2[Medium Risk Context]
D1 --> C3[High Risk Context]
C1 --> S1[Standard Protocols]
C2 --> S2[Enhanced Monitoring]
C3 --> S3[Strict Safeguards]
S1 --> O1[Normal Operation]
S2 --> O2[Cautious Operation]
S3 --> O3[Restricted Operation]
C3 --> E[Emergency Stop]
classDef ai fill:#FF8000,stroke:#333,stroke-width:3px,color:#fff
classDef context fill:#42A5F5,stroke:#333,stroke-width:2px,color:#fff
classDef safety fill:#66BB6A,stroke:#333,stroke-width:2px,color:#fff
classDef operation fill:#FFA726,stroke:#333,stroke-width:2px,color:#fff
classDef emergency fill:#F44336,stroke:#333,stroke-width:3px,color:#fff
class AI ai
class C1,C2,C3 context
class S1,S2,S3 safety
class O1,O2,O3 operation
class E emergency
Knowledge graph construction benefits enormously from conditional logic principles. When we build a knowledge graph, we're creating networks of conditional relationships: "If entity A has property B, then it likely relates to entity C in way D." The variably strict approach helps us model these relationships with appropriate context sensitivity.
In AI prompt engineering, I've found that leveraging variably strict conditional thinking dramatically improves results. Instead of rigid "if-then" prompts, we craft contextually sensitive conditionals: "Given context X, if the user asks Y, then respond with approach Z." This mirrors how natural language conditionals work—their strength and applicability shift based on conversational context.
Practical Implementation Strategy
The key to applying conditional logic principles practically is to:
- Identify the relevant contexts that affect conditional strength
- Map similarity relations between different scenarios
- Build flexibility into conditional rules to accommodate context shifts
- Use visual tools to make these relationships transparent and adjustable
PageOn.ai's Vibe Creation feature excels at building visual decision trees that capture the essence of possible worlds reasoning. By creating interactive models that show how context shifts affect conditional truth values, we can build decision support systems that are both logically rigorous and practically useful.
Visualizing Complex Conditional Relationships
When I work with complex conditional relationships, I've learned that visualization isn't just helpful—it's essential. The human mind struggles to track multiple nested conditionals and their interdependencies without visual aids. This is where the art and science of conditional logic visualization truly shines.
Techniques for Nested Conditional Structures
Representing nested conditionals requires a layered approach. I think of it like creating a 3D map where each layer represents a different level of conditional depth. The challenge is maintaining clarity while showing the intricate relationships between conditions at different levels.
Conditional Nesting Complexity Levels
Creating interactive models that show how context shifts affect conditional truth values has become one of my favorite applications of this work. These models allow users to manipulate contextual parameters and immediately see how those changes ripple through the conditional network. It's like having a flight simulator for logical reasoning.
Interactive Conditional Truth Model
This model shows how changing context parameters affects conditional evaluation:
graph TB
subgraph "Context Layer"
C1[Economic Context]
C2[Social Context]
C3[Technical Context]
end
subgraph "Primary Conditionals"
P1[If A then B]
P2[If C then D]
P3[If E then F]
end
subgraph "Secondary Conditionals"
S1[If B and X then G]
S2[If D and Y then H]
S3[If F and Z then I]
end
subgraph "Truth Values"
T1[Strong True]
T2[Weak True]
T3[Indeterminate]
T4[Weak False]
T5[Strong False]
end
C1 --> P1
C2 --> P2
C3 --> P3
P1 --> S1
P2 --> S2
P3 --> S3
S1 --> T1
S1 --> T2
S2 --> T2
S2 --> T3
S3 --> T3
S3 --> T4
classDef context fill:#E3F2FD,stroke:#1976D2,stroke-width:2px
classDef primary fill:#FFF3E0,stroke:#F57C00,stroke-width:2px
classDef secondary fill:#E8F5E8,stroke:#388E3C,stroke-width:2px
classDef truth fill:#FCE4EC,stroke:#C2185B,stroke-width:2px
class C1,C2,C3 context
class P1,P2,P3 primary
class S1,S2,S3 secondary
class T1,T2,T3,T4,T5 truth
Mapping exception cases and edge conditions requires special attention to boundary conditions where our normal similarity judgments break down. I've found that these edge cases often reveal the most about how conditional logic actually works in practice. They're the stress tests that show where our logical frameworks need refinement.
Exception Handling in Conditional Logic
Exception cases typically arise when:
- Multiple contexts suggest conflicting similarity orderings
- The antecedent of a conditional is inconsistent with background assumptions
- Nested conditionals create logical loops or contradictions
- Context updates lead to unstable or oscillating truth values
Visualizing these exceptions helps us understand not just when our logical systems fail, but why they fail and how we might design more robust alternatives.
PageOn.ai's AI Blocks feature excels at constructing modular representations of conditional chains. Instead of trying to visualize everything at once, we can build up complex conditional structures piece by piece, each block representing a manageable logical component. This modular approach makes it possible to understand and work with conditional systems that would otherwise be incomprehensibly complex.
What I find most rewarding about developing visual frameworks for abstract logical concepts is watching them become accessible to non-specialists. When a complex philosophical idea becomes a clear, interactive diagram, we're not just making it easier to understand—we're opening up new possibilities for practical application and creative insight.
Bridging Theory and Practice
The ultimate test of any theoretical framework is its practical utility. Throughout my exploration of variably strict conditionals, I've been continually amazed by how these abstract concepts illuminate real-world problems across diverse domains. Let me share some case studies that demonstrate this power in action.
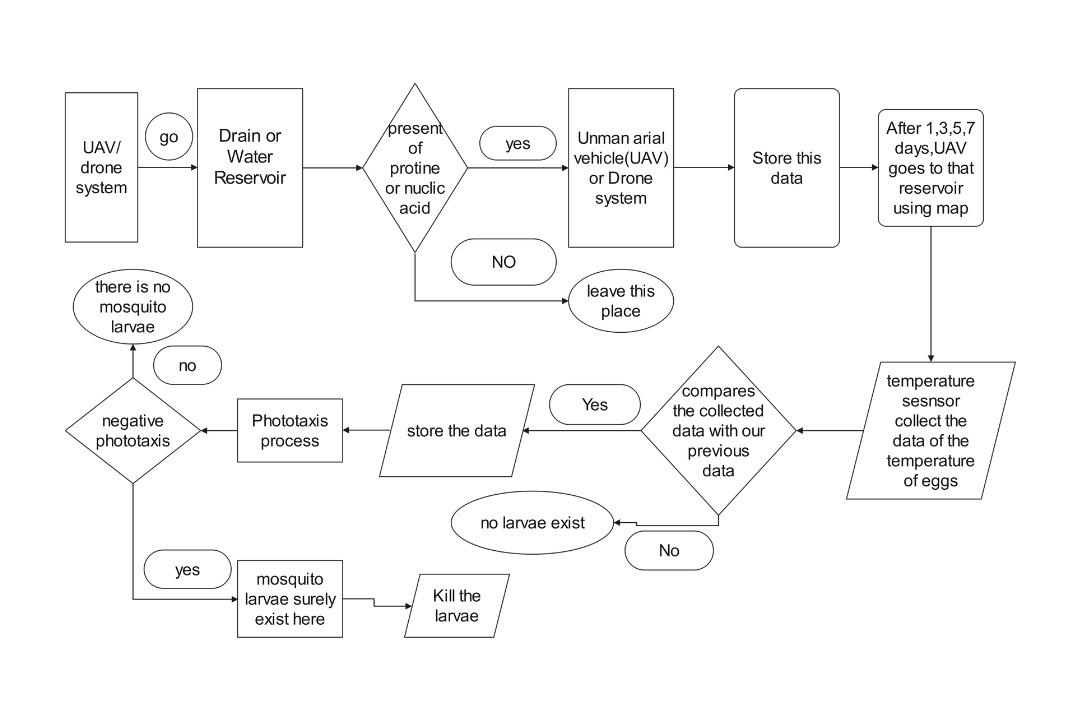
Case Study: Medical Diagnosis Systems
In medical diagnosis, we constantly work with conditionals like "If symptom A is present, then condition B is likely." But the strength of these conditionals varies dramatically based on patient context—age, medical history, environmental factors. A variably strict approach helps us build diagnostic systems that appropriately weight symptoms based on individual patient similarity to known cases.
Diagnostic Conditional Strength by Patient Context
In financial risk assessment, I've seen how conditional logic transforms our understanding of market relationships. Traditional models often rely on fixed correlations, but variably strict conditionals help us understand that the relationship between events depends heavily on market context. "If tech stocks fall, then the whole market falls" might be strongly true in some contexts and weakly true in others.
Integration Strategy Framework
Here's how to systematically integrate conditional reasoning into existing knowledge systems:
flowchart LR
subgraph "Assessment Phase"
A1[Identify Existing Conditionals]
A2[Map Context Dependencies]
A3[Evaluate Current Rigidity]
end
subgraph "Design Phase"
D1[Define Similarity Metrics]
D2[Create Context Sensors]
D3[Build Update Mechanisms]
end
subgraph "Implementation Phase"
I1[Pilot Testing]
I2[Gradual Rollout]
I3[Performance Monitoring]
end
subgraph "Optimization Phase"
O1[Feedback Analysis]
O2[Context Refinement]
O3[System Evolution]
end
A1 --> A2
A2 --> A3
A3 --> D1
D1 --> D2
D2 --> D3
D3 --> I1
I1 --> I2
I2 --> I3
I3 --> O1
O1 --> O2
O2 --> O3
O3 --> A1
classDef assessment fill:#E3F2FD,stroke:#1976D2,stroke-width:2px
classDef design fill:#FFF3E0,stroke:#F57C00,stroke-width:2px
classDef implementation fill:#E8F5E8,stroke:#388E3C,stroke-width:2px
classDef optimization fill:#FCE4EC,stroke:#C2185B,stroke-width:2px
class A1,A2,A3 assessment
class D1,D2,D3 design
class I1,I2,I3 implementation
class O1,O2,O3 optimization
The tools and methodologies for applying conditional logic insights have evolved tremendously. I've developed a systematic approach that begins with identifying existing conditional relationships in a system, mapping their context dependencies, and then gradually introducing variably strict evaluation mechanisms. The key is to start small and scale up as confidence builds.
Methodology: The SMART Integration Approach
- Survey: Identify existing conditional relationships in your system
- Map: Document context dependencies and similarity relations
- Adapt: Introduce flexibility into rigid conditional rules
- Refine: Continuously adjust based on performance feedback
- Transform: Scale successful implementations across the organization
Looking toward future directions, I'm excited about how visual representation of logical structures enhances not just understanding, but discovery. When we can see the structure of our conditional reasoning, we often notice patterns and opportunities that were invisible in purely textual or mathematical representations. This visual approach opens up new avenues for both theoretical development and practical innovation.
PageOn.ai's Agentic capabilities represent a particularly promising frontier for transforming complex logical relationships into clear, actionable visual narratives. By leveraging AI to automatically identify conditional structures, map context dependencies, and generate appropriate visualizations, we can make sophisticated logical reasoning accessible to anyone who needs to understand and work with complex conditional relationships.
Future Vision: Automated Conditional Logic Visualization
I envision a future where AI systems can automatically detect conditional logic patterns in natural language, formal specifications, or data relationships, then generate appropriate visualizations that help humans understand and work with these patterns more effectively. This would democratize access to sophisticated logical reasoning tools and open up new possibilities for human-AI collaboration in complex problem-solving.
Transform Your Visual Expressions with PageOn.ai
Ready to turn complex logical concepts into clear, compelling visual narratives? PageOn.ai's powerful visualization tools can help you create intuitive representations of even the most abstract conditional relationships, making complex ideas accessible and actionable.
Start Creating with PageOn.ai TodayYou Might Also Like
Building Trust in AI-Generated Marketing Content: Transparency, Security & Credibility Strategies
Discover proven strategies for establishing authentic trust in AI-generated marketing content through transparency, behavioral intelligence, and secure data practices.
Google's 9-Hour Prompt Engineering Path to AI Mastery | Complete Visual Guide
Master AI communication through Google's comprehensive 9-hour prompt engineering framework. Learn visual strategies for effective AI interaction and professional success.
Prompt Chaining Techniques That Scale Your Business Intelligence | Advanced AI Strategies
Master prompt chaining techniques to transform complex business intelligence workflows into scalable, automated insights. Learn strategic AI methodologies for data analysis.
Transform Your AI Results by Mastering the Art of Thinking in Prompts | Strategic AI Communication
Master the strategic mindset that transforms AI interactions from fuzzy requests to crystal-clear outputs. Learn professional prompt engineering techniques that save 20+ hours weekly.
